Förderhöhe & hydrostatischer Druck
Wenn es darum geht, für eine ausgefallene Kühlmittelpumpe Ersatz zu finden, dann sollte die neue Pumpe natürlich den sie erwartenden Anforderungen genügen. Eine zu klein dimensionierte Pumpe wird permanent überlastet und hat eine entsprechend geringe Standzeit. Wahrscheinlich wird sie dann auch ihrer Aufgabe, nämlich ausreichend Kühlmittel zu fördern, in nicht zufriedenstellendem Umfang gerecht werden können.
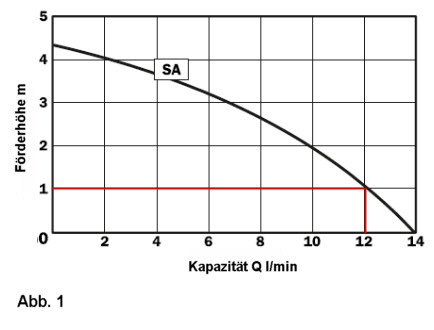
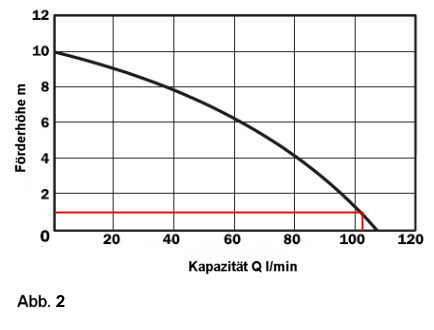
Immer wieder stellt sich die Frage nach dem erforderlichen Druck, welche die Pumpe aufbauen muss. Bei Kühlmittelpumpen, welche meist im Niederdruckbereich (kleiner 1 bar) arbeiten, und welche selten Förderhöhen größer als 1,5 Meter bewältigen müssen, ist die Frage nach dem Druck zweitrangig. Wichtiger in diesem Zusammenhang ist die Kapazität, also die maximale Fördermenge. Natürlich hängt diese auch von der Förderhöhe ab. Da diese, wie erwähnt meist gering ist, fällt sie und damit auch der Druck als Kriterium entsprechend weniger ins Gewicht. Zur Veranschaulichung können Fig. 1 und 2 hergenommen werden.
Ein wenig Physik
Gehen wir näher auf das Verhältnis zwischen Druck (p) und Förderhöhe (H) ein. Wikipedia fasst zusammen:
Unter der Förderhöhe H einer Flüssigkeitspumpe versteht man die nutzbare Arbeit, die von der Pumpe auf das Fördermedium übertragen wird, bezogen auf das Gewicht des Mediums; es handelt sich also um eine spezifische Größe.
Quelle: Wikipedia
Und zum Thema Druck:
Der hydrostatische Druck … ist der Druck, der sich innerhalb eines ruhenden Fluids, das ist eine Flüssigkeit oder ein Gas, durch den Einfluss der Gravitation einstellt.
Quelle: Wikipedia
Man differenziert Druck in Abhängigkeit des Kontextes; hier betrachten wir den hydrostatischen Druck, da wir es mit Flüssigkeiten zu tun haben. Um eine Flüssigkeit emporzuheben, muss eine Pumpe eine gegen die Erdbeschleunigung gerichtete Arbeit verrichten; der so von der Pumpe erzeugte Druck wird als Förderdruck bezeichnet. Je höher nun die Wassersäule ist, desto höher muss der Förderdruck der Pumpe sein, um gegen den hydrostatischen Druck anzuarbeiten. Betrachten wir das für die Flüssigkeit Wasser, so kann man nach dem pascalschen Gesetz schreiben:
p(h) = ρgh + p0Formel 1
p(h) = hydrostatischer Druck in Abhängigkeit von der Höhe der Wassersäule
ρ = Dichte [für Wasser: ρ ≈ 1.000 kg/m³]
g = Erdbeschleunigung [für Deutschland: g ≈ 9,81 m/s²]
h = Höhe der Wassersäule
p0 = Luftdruck auf Flüssigkeitsoberfläche
In obiger Formel ist der Luftdruck, welcher zusätzlich auf der Wassersäule lastet, mit betrachtet. Das ist physikalisch korrekt und immerhin beträgt er auf Normalnull (NN, Meeresspiegel) ca. 1 bar (1013,25 hPa, zu den Einheiten s.u.) In der Praxis kann dieser jedoch vernachlässigt werden, da er auf alle Körper und in jede Richtung gleich wirkt. (Druck ist eine skalare, also ungerichtete Größe).
Einheiten für den Druck
Um die physikalische Theorie in anwendbare Praxis zu übersetzen, betrachten wir die Einheiten des hydrostatischen Drucks. Wikipedia:
Die Physikalischen Einheiten für den hydrostatischen Druck sind:
Quelle: Wikipedia
international die SI-EinheitPascal (Pa): 1 Pa = 1 N/m²;
zudem in Deutschland und Österreich die „gesetzliche Einheit“Bar (bar): 1 bar = 100.000 Pa bzw. N/m² (= 100 kPa)
Zur Beschreibung des hydrostatischen Drucks wird zum Teil auch noch die nicht-SI-konforme veraltete Maßeinheit Meter Wassersäule(mWS) verwendet.
Sehen wir auf den Zusammenhang zwischen Pascal und bar, so erkennen wir, dass 1 bar 100 Kilopascal oder 1000 Hektopascal (hPa) entspricht. Die Einheit Hektopascal kennen Sie vielleicht aus dem Wetterbericht, denn sie wird gerne von Meteorologen genutzt, um den Luftdruck (aerostatischer Druck) zu beschreiben. 1013 hPa, also ca. 1 bar, entsprechen dem Normaldruck auf Meereshöhe. Da der Druck auf alles gleichermaßen wirkt und in unserem Beispiel der Druckunterschied von NN auf 10 m sehr gering ist, kann der atmosphärische Druck vernachlässigt werden.
Die veraltete Maßeinheit mWS (Meter Wassersäule) ist zwar nicht SI-konform, hilft uns in der Praxis aber sehr schön weiter, da:
1 bar = 10 mWS = 100.000 Pa = 100.000 N/m²
Daraus lässt sich die einfache Faustformel für Wasser (oder Stoffe gleicher Dichte, Kühlschmiermittel bestehen zu über 90% aus Wasser und können dazugezählt werden) ableiten:
1 bar ≙ 10 Meter FörderhöheMit einem Pumpendruck von 1 bar lässt sich eine Wassersäule von 10 Metern erzeugen.
Natürlich ist das nur ein Näherungswert und es ist vor Allem auch die Reibung in Rohr, Schlauch, Stutzen etc. zu berücksichtigen; für die Praxis ist diese Formel aber ausreichend und es lässt sich gut damit rechnen. Aber warum entsprechen 10 mWS einem bar bzw. 100 kN/m²? Sie ahnen es wahrscheinlich!? Klar, dahinter steckt das Maß der Erdbeschleunigung, welche mit annähernd 10 m/s² zu Buche schlägt. Pflegen wir Werte und Einheiten in die Formel 1 ein und vernachlässigen wir den Druck der Atmosphäre (s.o.), erhalten wir:
100 kN/m² = 1.000 kg/m³ x 10 m/s² x 10 m
stellen wir die Formel nach h um ergibt sich:
10 m = 100 kN/m² / (1.000 kg/m³ x 10 m/s² )
Die Kühlmittelpumpe PA-150, deren Kennlinie der Abbildung 2 zu entnehmen ist, kann bis zu einer Höhe von 10 m fördern, erzeugt also einen maximalen Pumpendruck von etwa 1 bar.